1.西安电子科技大学 数学与统计学院, 西安 710071) 2.西安电子科技大学 人工智能学院, 西安 710071)
摘 要 利用线性规划的对偶理论给出了求解线性规划的三种方法.
关键词 线性规划;最优解;最优基;对偶理论;互补松弛条件
中图分类号G642文献标识码 A
当我们拿到一道题目,根据问题的特点可以找出一种求解方法得到答案,但有时可以尝试从不同角度对该题目进行进一步探讨和研究,即“一题多解”. 本文以求解一道线性规划问题的最优解为例从不同角度探讨了该问题的多种解法[1-6].
例[2]:已知如下的线性规划问题(1),求其对偶问题的最优解.
 (1)
(1)  (2)
(2)
解:由于问题(1)的约束均为小于等于型不等式,且右端均为非负数,引入松弛变量![]() ,将其化为标准型时易于到它的一个基本可行解,为此考虑先求出问题(1)最优解,然后再求其对偶问题(2)的最优解.
,将其化为标准型时易于到它的一个基本可行解,为此考虑先求出问题(1)最优解,然后再求其对偶问题(2)的最优解.
法1(公式法)先对问题(1)引入松弛变量![]() 将其化为标准型,从该问题的一个基本可行解出发,用单纯形法求得问题(1)的最优单纯形表如表1,则可用公式法
将其化为标准型,从该问题的一个基本可行解出发,用单纯形法求得问题(1)的最优单纯形表如表1,则可用公式法![]() 求对偶问题(2)的最优解,其中
求对偶问题(2)的最优解,其中![]() 为原问题的最优基矩阵,这里
为原问题的最优基矩阵,这里

![]() ,
,
故  .
.
注:若原问题易于用单纯形法迭代求解,则从其最优 表1 问题(1)的最优单纯形表
单纯形表中可直接写出原问题的最优基矩阵及其逆矩阵,此时用公式法求对偶问题的最优解比较简单,但当最优基矩阵阶数较大时,会面临求解其逆矩阵困难的问题.
法2(表上直接读出对偶问题的最优解) 若通过单纯形法求得原问题(1)的最优解,此时也可从表上读出对偶问题的最优解.理由如下[1],不失一般性,原问题(1)可写为如下抽 象形式 (3),并将(3)化为标准形式,记为(4) .
基金项目:2021年西安电子科技大学研究生课程思政示范建设建设项目.2023年最优化方法课程思政探索项目.
 (3)
(3) 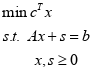 (4)
(4)  (5)
(5)
设(4)有最优解时对应的最优基为![]() ,此时检验数
,此时检验数![]() ,且
,且![]() ,即
,即
![]() (*)
(*)
记(3)的对偶问题为(5),在(*)中令![]() ,则
,则![]() 为(5)的可行解,此时(5)的目标函数值为
为(5)的可行解,此时(5)的目标函数值为![]() ,而(3)在最优解处对应的最优值为
,而(3)在最优解处对应的最优值为![]() ,(3)和(5)的目标函数值相等,故
,(3)和(5)的目标函数值相等,故![]() 为(5)的最优解,而
为(5)的最优解,而![]() 的值从表中看,刚好为松弛变量
的值从表中看,刚好为松弛变量![]() 对应的检验数,从表1可直接读出,
对应的检验数,从表1可直接读出,![]() ,故对偶问题(2)的最优解为
,故对偶问题(2)的最优解为![]() .
.
注:若通过单纯形法求得原问题的最优解,也可从原问题的最优单纯形表中读出对偶问题的最优解,但该方法对知识掌握的要求较高,需要指出的一点是,若所给原问题不是(3)的形式,则需要进行相应的推导.
法3(利用互补松弛条件)由图解法易知,问题(1)的最优解为![]() ,可利用互补松弛条件求出其对偶问题(2)的最优解.由于原问题(1)的最优解中
,可利用互补松弛条件求出其对偶问题(2)的最优解.由于原问题(1)的最优解中![]() ,故对偶问题中相应的约束在对偶问题的最优解
,故对偶问题中相应的约束在对偶问题的最优解![]() 处均取等号,即
处均取等号,即

联立解得![]() ,故对偶问题(2)的最优解为
,故对偶问题(2)的最优解为![]() .
.
注:该方法比较简单,但对知识掌握的程度要求较高.该方法只需求解线性方程组就可以求出对偶问题的最优解,但前提是必须知道原问题的最优解,同时需要理解线性规划的互补松弛条件的含义.
本文从求解一道线性规划问题出发,尝试从不同角度、方法、途径,根据笔者对题目的理解及考虑问题的常见思路出发,给出了求解线性规划问题的对偶问题的三种方法,这些方法借助对偶问题与原问题的相关性质求线性规划的最优解,对知识掌握的要求较高,但是通过对不同方法的使用,可以培养学生的创新思维、创新意识[6]、发散思维和综合运用知识的能力,在一定程度上可以培养学生运用辩证主义的观点和立场去分析、评价和解决问题,由此,引导学生在学习、生活中遇到困难可以多方位、多角度考虑问题,从而找到解决问题的有效途径.
参考文献
[1] 陈宝林. 最优化理论与算法. 清华大学出版社,北京,2005.
[2] 陈开周. 最优化计算方法.西安电子科技大学出版社,西安,1985.
[3] 解可新,韩立新等. 最优化方法. 天津大学出版社,天津,1997.
[4] 唐焕文,秦学志. 实用最优化方法(第三版).大连理工大学出版社,大连,2004.
[5] 谢政,李建平等. 非线性最优化. 国防科技大学出版社,2003.
[6] 吴飞,赵俊芳,廉海荣.“最优化方法”课程思政案例设计及其实现. 中国地质教育,2023年第1期,72-75.
![]()