无单元 Galerkin 方法数值求解二维瞬态热传导问题-中国期刊网

首页 > 《银幕内外》 > 2020年1期 > 无单元 Galerkin 方法数值求解二维瞬态热传导问题

（整期优先）网络出版时间：2020-10-10

作者: 王红

文化科学 >新闻学

打印

同系列资源

/ 3

无单元 Galerkin 方法数值求解二维瞬态热传导问题

王红

重庆师范大学，重庆沙坪坝， 401331

摘要：采用无单元 Galerkin 方法数值求解具有狄利克雷边界条件的二维瞬态热传导问题。首先离散该问题的时间变量，将该问题转化为与时间无关的边值问题；然后采用罚函数法处理 Dirichlet 边界条件，得到数值离散方程组，再利用 Matlab 软件求解给出的算例，结果表明该方法得到的数值结果与解析解吻合较好，该方法具有较高的计算精度和较好的收敛性。

关键词：二维瞬态热传导问题；无单元 Galerkin 方法；罚函数法； Matlab 软件中图分类号：G210.7 文献标识码：A 文章编号：20200168685

有限差分法（FDM）[1]、有限元法（FEM）[2]、边界元法（BEM）得

[3]、无网格法[4]等数值方法是解决瞬态热传导问题的常用方

 ____T^k^¹ _

____Tk 1 __

法。Burlayenko 等人[5]用梯度有限元法计算了梯度材料中的瞬_T ^^k^¹^vd    __k^__vd   _k ^  vd  ^

^y ^²y ^_

态温度。Sutradhar 和 Paulino[6]提出了一种简单的边界元法，该法只考虑边界条件，适用于梯度材料中的三维非定常热传导问

 _T ^^k^¹^vd   _^k^¹Q vd  ^^



^k^¹_vd_

题。Sladek 等人[7]用无网格局部边界积分方程方法考虑梯度材料中的不稳定温度场。

无单元 Galerkin 方法是应用最为广泛的无网格方法之一。本文借鉴文献[8]应用无单元 Galerkin 方法数值求解具有狄利克雷边界条件的二维瞬态热传导问题。首先离散该问题的时间变

量，将该问题转化为与时间无关的边值问题；然后采用罚函数法

  

（7）

Í¼Æ¬ 16

接下来，根据高斯公式化简（7）式，于是得与混合边值问





题（6）等价的变分问题：求_T^k^¹ __x___H1 ___，使得，有

处理 Dirichlet 边界条件，得到数值离散方程组，再利用 Matlab 软件求解给出的算例，最后给出了一个数值算例来验证理论误差a _T ^^k^¹^,v_

 

（8）T^^k^¹^vd



vQ^^k^¹^d



R^^k^¹^vd vT^^k^²^d

 

结果。

二维瞬态热传导方程总的来说，在具有空间变导率的各向同性固体中，二维瞬态其中双线性形式被定义为

__T^k^¹ __v

a _T^^k^¹^,v_ vT^^k^¹^d k ^d

^T v^k^¹

_^k^¹ _

k^d vT d

导热的控制方程为：^^_^x x_²y y_^

^^T^ ^^T ^^^^T^

   设为基于节点__x_^N构造的移动最小二乘（Moving Least

^^ 

^c^__t^__x_^k₁__x_^__y_^k₂__y_^^Q^,^x^,^y^^^,

（1）

方程（1）的初始条件ⁱi1

Squares ， MLS ）近似形函数，在无网格近似解空间

^V_h^ ^^s^p^aⁿ^_i^,1^ⁱ^^N^{中，变分问题}^（⁸^）^{式可近似为：求，}

^T^^k^¹^^x^^V^^使得^^v^x^^V^^，有

^T^x^,⁰ ^^^x^，^^T^x^,^t_

⁼^^x^，^x^^，^h h h



（2）

__tt 0 2

a _T ^^k^¹^, v _

T ^^k^¹^vd  vQ^^k^¹^d  

 

_vT^k^¹_d_



Dirichlet 边界条件

T  T ， on ，^（³^）

（9）



^其中^T^^k^¹^^x ^^M

_T^k^¹ _

_x_____T^k^¹ _，将_v__x__依次

其中代表温度，表示材料密度，代表比热容，表示发热率，、分别指沿、方向的热传导系数。

无单元 Galerkin 法数值求解二维瞬态热传导问题h i i

i1

取为_₁_,_₂_,_…,__N，则（6）式可以离散为如下方程组：

为了离散时间变量，我们在时间 t 处进行泰勒展开，从而^K^

___G__T^k^¹ ___GT^k^¹ __b^k _，_k=1，2，_⋯_（10）

成微分商 _其中

T ^T^^k^¹^^x^^T^^k^¹^^x

_2 _'''_T ^^ ^^

t ^2 6__t''' ^^ij^^¹ x  x^^² y  y_ⁱ^j

（4）

其中为时间变量的步长，，且^G_ij^__^_i^_j^d^^，

^T^^k^^x ^^T^x^,^y^,^k^^，^{k=0，1，2，}^⋯

^k __^^k^¹^d   T^^k^¹^d 

我们在点考虑方程（1），结合方程（1）~（3）得___ⁱ

数值算例_ⁱ

_^k^¹

 ^__T^k^¹ _  ^__T^k^¹ _^k^¹ ^k^¹ ^k^¹考虑没有热量产生的热传导方程：

 __x_k₁x ^^y ^^k²__y_ TQ  RT  T  T

，（5）

其中__^c^，对于正常数 C 有 _R^^k^¹^__C_²。

   0，

t x² y²

^x^^{0, 1}^，^y^^{0, 1}^，

2

显然，方程（5）的迭代求解需要初始值，根据（4）式可得

T ^^¹^ T ^¹^ 2 _x_ o _³_，x  ，

Í¼Æ¬ 17

令（5）式中 k=0，得，接下来采用罚函数法处理狄利克雷边界条件，则问题（1）~（3）可转化为与时间无关的混合边值问题：

（6）

_其中_f^k ___T^k^¹ __Q^k^¹ __R^k^¹_{。k=1，2，}_⋯

^以_v__x___H¹___^{乘微分方程（6）的两端，并在} ^上积分

该问题的初始条件、狄利克雷边界条件满足解析解。

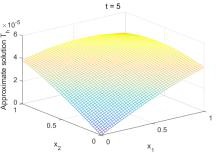
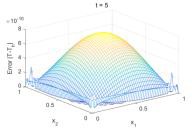
图 1 t=0.5 时的数值解和误差图

图 1 给出了当节点间距 h=0.02，时间步长τ=0.01，t=0.7s 时用无单元 Galerkin 方法求解得到的数值解与误差图，其中最大误差小于 10-6，此结果表明数值解与解析解具有很好的一致性，该方法具有较高的计算精度。

结论

针对二维瞬态热传导问题，本文采用无单元 Galerkin 方法

散该问题的时间变量，将该问题转化为与时间无关的边值问题；然后采用罚函数法处理 Dirichlet 边界条件，得到数值离散方程组，再利用 Matlab 软件求解给出的算例，结果表明该方法得到的数值结果与解析解吻合较好，该方法具有较高的计算精度和较好的收敛性。

参考文献：

Annafi T A, Gyeabour A A, Akaho E H K, et al. Finite difference analysis of the transient temperature profile within GHARR-1 fuel element[J]. Annals of Nuclear Energy, 2014, 68: 204-208.
S. Khajehpour, M. R. Hematiyan, and L. Marin. A domain decomposition method for the stable analysis of inverse nonlinear transient heat conduction problems[J]. Heat Mass Transfer, 2013, 58: 125-134.
Chen J T, Yueh C Y, Chang Y L, et al. Why dual boundary element method is necessary?[J]. Engineering Analysis with Boundary Elements, 2017, 76: 59-68.
Y. Gu, L. Wang, W. Chen, C. Z. Zhang. Application of the meshless generalized finite difference method to inverse heat source problems[J]. Heat Mass Transfer, 2017, 108: 721–729.

Burlayenko V N, Altenbach H, Sadowski T, et al. Modelling functionally graded materials in heat transfer and thermal stress analysis by means of graded finite elements[J]. Applied Mathematical Modelling, 2017, 45(5): 422-438.
Sutradhar A, Paulino G H. The simple boundary element method for transient heat conduction in functionally graded materials[J]. Computer Methods in Applied Mechanics & Engineering, 2004, 193 (42-44): 4511-4539.
Sladek J, Sladek V, Zhang C. Transient heat conduction analysis in functionally graded materials by the meshless local boundary integral equation method[J]. Computational Materials Science, 2003, 28 (3-4): 0-504.
Li X,Zhang S, Wang Y,et al. Analysis and application of the element-free Galerkin method for nonlinear sine-Gordon and generalized sinh-Gordon equations[J]. Computers & Mathematics with Applications, 2016, 71(8): 1655-1678.